Tesla Motors

[omgwtfbyobbq]

The EPA highway test schedule is in fact ~48.3mph average with one stop at the end.

While the tesla site may be down, iirc range was using the EPA's highway cycle. I went over the calcs again and I'm pretty sure they're using the Lotus Elise' (~17.5ft^2) reference area with a Cd of ~.23.

The force in newtons require to move the car at 48.3mph is roughly, W*Crr+.5(ro)V^2(CdA), without sliding friction. But, it's not much in most expression I've seen (~20N), so we can leave it. W=2500lbs, Crr=.015 (sticky, sticky tires), CdA=4.1ft^2, V=48.3mph and ro=.075lb/ft^3 (sea level), so we get...
Rolling friction~40N
Fluid friction~360N
So total drag is ~400N. Now we're going 48.3mph~21.6m/s, so power is 8.64kw. If this vehicle has a range of 250miles@48.3mph then it takes 5.17hours to travel this distance. So we're left with ~45kwh required at the wheels, but we have drivetrain losses as you suggested, and ~18% seems *reasonable. 45kwh/.82=~55kwh of battery and everything seems to match up. I have to say, you lost me after that 375 showed up, I have no clue where that came from!


*They stated the motor was ~90% efficient iirc, so as long as bearing losses are ~10%, you're spot on.

Edit-Forgot to convert lbf to N, ack, .454 would've helped a bit! Can't mix and match units in any case...

[The Toecutter]

I think you goofed your units on calculating drag at that speed. It is nowhere near 400N at 48 mph.

Your rolling force for instance, .015 * 2,500 pounds gives you 37.5 pounds rolling force, which is 166.8 Newtons. Way different than the 40 N you post.

As for aero drag, .5(ro)V^2(CdA)
= .5 * .075 lb/ft^3 * 21.6 m/s * 21.6 m/s * 17.5 ft^2 * .23
= 70.4214 lb/ft * m^2/s^2
= 31.9589 kg/ft * m^2/s^2
= 104.85203 kg/m * m^2/s^2
= 104.85 kg*m/s^2
= 104.85 N

So 105 N aero + 167N rolling = 272 N of drag, way less than the 400 you post.

I think you screwed your units up.



If I do it in horsepower, feet, mph, ect., and even plug it into Uve's EV Calculator(http://www.geocities.com/hempev/EVCalculator.html), my numbers end up working out very close to what I had posted earlier insofar as power requirements.

Lets try this in metric working with metric from the start.

I'll use the Cd*A reference you provide and the 18% transmission loss, the rho value(~1.25kg/m^3), and 20N sliding friction.

Mass(W): 1,135 kilograms
Drag Coefficient(Cd): .23
Frontal Area(A): 1.63 square meters
Rolling Resistance Coefficient(Cr): .015
Transmission Efficiency(TE): .82
Motor Efficiency(ME): .90
Battery Capacity(C): 55,000 Wh

Velocity(V): expressed in meters per second
Force Drag(FD): expressed in newtons
Force Rolling(FR): expressed in newtons
Force Sliding(FS): 20 newtons
Wheel Power(WP): expressed in watts
Motor Power(MP): expressed in watts
Battery Power(P): expressed in watts
Run Time(T): expressed in hours

Air Density(Rho): 1.25 kg/m^3
Gravitational Constant(G): 9.8 N/kg


Equations used:

FD = .5 * Rho * Cd * A * V^2
FR = Cr * W * G

WP = (FD + FR + FS) * V
MP = WP / TE
P = MP / ME

T = C / P

Results:

At 21.6 m/s(48 mph):

FD = 109
FR = 167
FS = 20
WP = 6,397
MP = 7,801
P = 8,668
T= 6.34

At 31.3 m/s(70 mph):

FD = 230
FR = 167
FS = 20
WP = 13,052
MP = 15,917
P = 17,686
T= 3.11


So at 48 mph, we get 6.34 hours of run time, or 304 miles range. At 70 mph, we get 3.11 hours of run time, or 218 miles range.

Check the units, they work out.

The results I arrive at are quite a bit different from the 250 mile range at the EPA cycle, are they not?

[omgwtfbyobbq]

Heh, dammit... I did the entire thing in english and forgot to convert the force to metric!
So, going backwards again, assuming a 55kwh pack and 82% efficiency, we're using 45kwh at the wheels. We'll keep this in metric since last time I f'd it up, 45kwh/5.17h=8.7kw, 8.7kw/21.6m/s=403N. So, since W*Crr=1134kgm/s^2*.015=17N, then fluid friction must be 403N-17N=386N. So... Like you said, at 75mph~33.5m/s, all of this makes sense since 386N=.5(1.2)(33.5^2)(1.65(Cd), which yields a Cd of ~.35. Which sounds exactly like a stock lotus elise... I wonder what the actual CdA is?

[The Toecutter]

My best educated guess is a Cd of .30 and a frontal area of 18 feet square. The Elise has a .36 Cd, and Tesla claims to have made the car more aerodynamic.

I'd think on level ground at 60-65 mph, it would achieve 250 miles range, assuming little to no stops or slowdowns. This would correspnd to 220 Wh/mile at that speed, which makes a lot more sense, as that's more typical of small EV sportscars with only mild attention paid to aerodynamics(By comparison, the GM EV1 got 140 Wh/mile, AC Propulsion TZero 150 Wh/mile, at that speed).

Or if you go the EPA cycle and factor in all the accelerations and slowdowns, as there still are quite a few to help waste energy. I could try to integrate that curve, and the 250 miles range would then make sense. The graph certaily doesn't show the steady speed that would be more representative of highway driving.

[omgwtfbyobbq]

That's something I was thinking about... Range shouldn't drop because of the combined cycle... It should actually increase. Take a diesel and a hybrid, the diesel gets about the same mileage in city driving as it does in highway because it doesn't suffer from pumping losses at lower rpm so engine efficiency is constant, and the hybrid gets better city because the regenerative brakes capture a large portion of energy that would otherwise be lost and allow it to be reused and it also doesn't waste any energy at stops/deceleration. An EV is the best of both worlds, no drop in engine efficiency wrt speed and regenerative braking... city mileage should own highway mileage. Anecdotally, in my diesel bunny I get the same mileage in city driving with a ~30mph average and all that idling/braking as I do on the freeway at ~50-55mph, so I could go off and make a statement like idling/braking wastes as much energy as going 50mph compared to 30mph does. If I had regenerative braking and an EV motor I'd probably get twice the city mileage I do now, even if the brakes only catch ~1/3-1/2 of the energy. Going 55mph compared to 30mph is still ~three times the energy, fluid drag is huge!

I sent them an email asking about range, but I doubt they'll respond. I figure they're deliberately understating the range because they'd rather not have people strand themselves if they're cruising along at 85-90mph or something like that. I wonder if they'll have a forum where people can post their distance traveled, conditions, and energy used?

Edit- Here's the EPA's city driving schedule

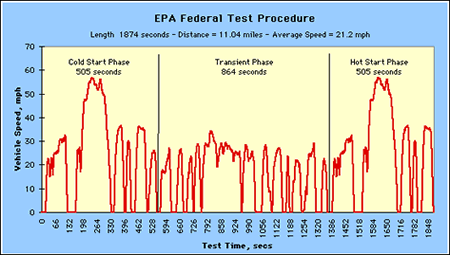
I think the best way to compare would be to take the average speed from each segment then take some fraction of the energy at the top speed of each segment for regenerative braking. Not sure how much energy it would capture, but we should be able to figure out the average consumption and range from that. It'd be very wishy washy and all that since the time intervals aren't well defined, but it's something. I wonder if we could contact the EPA and get better info?

[The Toecutter]

Regenerative braking will only recover 10-30% of lost kinetic energy. Further, AC motors/inverters do not see increased efficiciency with increased load like internal combustion engines do.

The lower aero drag seen at lower speeds will only be noticed if the speed is kept constant. Frequent and repeated acceleration/deceleration is actually one of the EV's least efficient operating points, and why so many attempt regen just to gain an extra 10% of so of range. Steady cruising is its most efficient. The EPA cycle, if you look at the time taken for each acceleration/deceleration, the car isn't coasting down to speed, it's actually braking, wasting lots of kinetic energy(although regen helps some). To drive an EV efficiently, you must coast.

[omgwtfbyobbq]

Wait.. a sec. Time to bust out some more of my four year old community college physniks!

Cruising at *25mph~11.17m/s, rolling friction is still the same 1123(.015)=17N, .5(1.2)(11.17^2)(1.65)(.35)=43N, so we use 60N to go 25mph. But it isn't just 60N, we also need to include the force used to accelerate the vehicle and apply the range of energy captured by the regen brakes. At rest this vehicle has zero kinetic energy, and at 25mph is has (.5)(116kg)(11.17^2)=7236W which, at an average of 11.17m/s is a total of 648N. So... Almost 700N, a lot of energy, of course the peak speed is higher, but then again we regain a fraction of the energy required in regen braking... Can anyone who's still in the know verify this?

*Since there are some stops, the ~20mph average isn't quite right. But there aren't that many stops, so it's in motion ~80-90% of the time with an average of maybe 25mph.

[The Toecutter]

Lets examine the energy lost slowing down and stopping in that 48 mph highway cycle for a minute.

I'm going to assume 50% of lost kinetic energy is recovered during the slow downs through regen. I'm going to neglect aero losses.

We have the following major speed drops from the EPA highway cycle graph:

-36 mph to 35 mph
-49 mph to 40 mph
-49 mph to 42 mph
-45 mph to 43 mph
-44 mph to 40 mph
-50 mph to 30 mph
-59 mph to 57 mph
-57 mph to 56 mph
-57 mph to 56 mph
-60 mph to 58 mph
-58 mph to 54 mph
-55 mph to 45 mph
-45 mph to 42 mph
-56 mph to 47 mph
-50 mph to 48 mph
-60 mph to 0 mph

I'm going to convert all of these to meters per second, and determine the total kinetic energy lost in joules assuming the 50% recaptured by regen and neglecting aero losses during acceleration/deceleration. It will be presented in a chart.

KE = .5 * M * V^2

KE is kinetic energy expressed in joules
M is mass in kilograms, the car being 1135 kg
V is velocity in m/s



If you add up all the kinetic energy lost, you get 628,341 J, assuming 50% has been recovered by regen.

To convert J to Wh, divide by 3,600, since 1 Wh is 1 Joule per second times 3,600 seconds.

So total Wh lost due to slowing down is 174.54 neglecting aero losses in acceleration/deceleration.

With aero losses, it would be a bit higher.

So that's at least 174.54 Wh lost over 765 seconds of travel at 48 mph average. At 48 mph, it takes 75 seconds to travel 1 mile.

So on average, every mile 17.11 additional Wh are being lost due to slowing down and stopping, completely neglecting aero losses involved in accelerating the car.

Aero losses in acceleration/deceleration would probably add about 50% to that, making it around 26 Wh/mile lost due to slowing down over that EPA highway cycle.


To put this in perspective regarding range, in theory by the calculations in my previous post had 304 miles range at a steady 48 mph, or 181 Wh/mile consumed at that speed. Add 26 Wh/mile to that consumption. That gives 207 Wh/mile.

Or with a 55 kWh pack, 266 miles range.


I think we found the reason for the descrepency. The other minor difference can be chalked up to things like crosswinds, which I didn't account for in my simulation.

From this, it's reasonable to conclude that the range at a steady 60-65 mph with few accelerations and decelerations would be about the same as the range following the EPA highway cycle.

[omgwtfbyobbq]

The car weighs ~1123N and has a mass of 1123N/9.8m/s^2=115kg. To move it to 48mph~21.5m/s requires .5(115kg)21.5m/s(21.5m/s)=26579kg(m^2/s^2) or ~26500J. Now assuming we capture ~30% of the energy via regen braking at the end, we only use 26579J(.7)=18605J. Since this test is ~765s, we use 18605J(1/765s)=24W. Compare this to your tesla glider with a Cda=5.4ft^2~.5m^2 and a Crr of .012, using a certain amount of energy per second. Rolling friction is 1123N(.012)=~14N, and fluid friction at 21.5m/s is .5(1.2kg/m^3)21.5m/s(21.5m/s).5m^2=139N, and a sum of 153N. At 21.5m/s, this glider uses 153N(21.5m/s)=3289W. This is huge when compared to the energy required to get the car to ~48mph.

During the city cycle, lets say the average speed is 25mph~11m/s, so using your glider again we get ~50N, or 550W. Now we have 23 accelerations to ~different speeds, which according to section, in m/s are [15,25,17,14,17,12],[12,12,11,13,15,13,13,13,11,10,13,10],[14,25,17,14,17]. The sum of the change in kinetic energy between a stop and these speeds is ~296522J, when considering regen braking it is ~207565J. The energy expended per second is 207565J/1874s=111W. Which is apparently nothing compared to the energy required to go ~50mph!

At 25m/s highway we use ~3300W, and at 11m/s in the city we use ~660W. Comparing these two in terms of efficiency can't be done unless we factor in speed, so if we were going the same distance per time, we need to use a factor of ~21.5mps/11mps=2.27. To compare the two we know that it'll take ~227% more time in the city, so over the same distance the EV in the city uses ~1500W... Which means that it's still twice as efficient as cruising at ~50mph is, but it's not the ideal situation where we're going half the speed and using a quarter of the energy. Braking in the EPA city cycle wastes at least twice as much energy as cruising does, probably more, which seems reasonable. And says a lot about how much gasoline engine efficiency drops at lower rpm imho... Of course radio, lights, heater, AC, etc... all add load.

Anyone see any problems?

[omgwtfbyobbq]

If you search for Tesla Motor's white paper, in the end they list the electricity consumption as being 110wh/km over the combined cycle. Assuming 90% mechanical (motor/bearing/transmission) efficiency, this means the glider requires ~99wh/km. Since we know the weight, and the EPA combined schedule, we can move backwards to isolate the CdA. Anyway, after futzing around I get that CdA=.416, which is very nice.